transform-function property CSS Reference

---

The <transform-function> CSS data type denotes a function to apply to an element's representation in order to modify it. Usually such transform may be expressed by matrices and the resulting images can be determined using matrix multiplication on each point.

Coordinates for 2D graphics

There are several coordinates model used when describing transformation. The most usual are the Cartesian coordinates and the homogenous coordinates.

Cartesian coordinates

In Cartesian coordinates each point of the Euclidian space is described using two values, the abscissa and the ordinate. The origin, the (0, 0) is the top-left corner of the element. Unlike the usual geometric convention, and like most cases in computer graphics, the y-axis goes to the bottom. Each point is mathematically described using the vector notation (x,y).

Each linear function is described using a 2x2 matrix like:

Applying the transformation consists in doing, for each point, the matrix multiplication between both:

It is possible to apply several transformations in a row:

With this notation, it is possible to describe, and therefore composite, most usual transformations: rotations, scaling or skewing. In fact all transformations that are linear functions can be described. One major transformation is not linear and therefore must be special-cased when using this notation: translation. The translation vector (tx, ty) must be expressed separately, as two more parameters.

Mobius homogenous coordinates in projective geometry

leading to 3x3 transformation matrices, though more complex and unusual for non-specialist, doesn't suffer from the translation limitation as these can be expressed as linear functions in this algebra, removing the need for special cases

Coordinates for 3D graphics

Functions defining transformations

matrix()

The matrix() CSS function specifies an homogeneous 2D transformation matrix comprised of the specified six values. The constant values of such matrices are implied and not passed as parameters; the other parameters are described in the column-major order.

matrix(a, b, c, d, tx, ty) is a shorthand for matrix3d(a, b, 0, 0, c, d, 0, 0, 0, 0, 1, 0, tx, ty, 0, 1).

Syntax

matrix(a, b, c, d, tx, ty)

Values

a b c d

Are <number> describing the linear transformation.

tx ty

Are <length> describing the translation to apply.

Cartesian coordinates on R2	Homogenous coordinates on RP2	Cartesian coordinates on R3	Homogenous coordinates on RP3
$\left(\begin{array}{cc}a& c\\ b& d\end{array}\right)$	$\left(\begin{array}{ccc}a& c& ty\\ b& d& tx\\ 0& 0& 1\end{array}\right)$	$\left(\begin{array}{ccc}a& c& ty\\ b& d& tx\\ 0& 0& 1\end{array}\right)$	$\left(\begin{array}{cccc}a& c& 0& tx\\ b& d& 0& ty\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right)$
	[a b c d tx ty]

matrix3d()

The matrix3d() CSS function describes a 3D transform as a 4x4 homogenous matrix. The 16 parameters are described in the column-major order.

Syntax

matrix3d(a1, b1, c1, d1, a2, b2, c2, d2, a3, b3, c3, d3, a4, b4, c4, d4)

Values

a1 b1 c1 d1 a2 b2 c2 d2 a3 b3 c3 d3 d4

Are <number> describing the linear transformation.

a4 b4 c4

Are <length> describing the translation to apply.

Cartesian coordinates on R2	Homogenous coordinates on RP2	Cartesian coordinates on R3	Homogenous coordinates on RP3
This transform applies to the 3D space and cannot be represented on the plan.		Cartesian-coordinate matrix doesn't allow to represent a generic 3d affine transforms as translations are not linear transforms.	$\left(\begin{array}{cccc}a1& a2& a3& a4\\ b1& b2& b3& b4\\ c1& c2& c3& c4\\ d1& d2& d3& d4\end{array}\right)$

rotate()

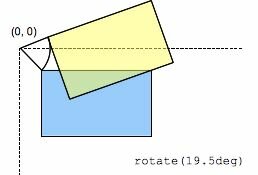The rotate() CSS function defines a transformation that moves the element around a fixed point (as specified by the transform-origin property) without deforming it. The amount of movement is defined by the specified angle; if positive, the movement will be clockwise, if negative, it will be counter-clockwise. A rotation by 180° is called point reflection.

Syntax

rotate(a)

Values

a

Is an <angle> representing the angle of the rotation. A positive angle denotes a clockwise rotation, a negative angle a counter-clockwise one.

Cartesian coordinates on R2	Homogenous coordinates on RP2	Cartesian coordinates on R3	Homogenous coordinates on RP3
$\left(\begin{array}{cc}cos(a)& sin(a)\\ -sin(a)& cos(a)\end{array}\right)$	$\left(\begin{array}{ccc}cos(a)& sin(a)& 0\\ -sin(a)& cos(a)& 0\\ 0& 0& 1\end{array}\right)$	$\left(\begin{array}{ccc}cos(a)& sin(a)& 0\\ -sin(a)& cos(a)& 0\\ 0& 0& 1\end{array}\right)$	$\left(\begin{array}{cccc}cos(a)& sin(a)& 0& 0\\ -sin(a)& cos(a)& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right)$
	[cos(a) -sin(a) sin(a) cos(a) 0 0]

rotate3d()

The rotate3d()CSS function defines a transformation that moves the element around a fixed axe without deforming it. The amount of movement is defined by the specified angle; if positive, the movement will be clockwise, if negative, it will be counter-clockwise.

In the 3D space, rotations have three degrees of liberty, describing an axis of rotation. The axis of rotation is defined by a [x, y, z] vector and pass by the origin (as defined by the transform-origin CSS property. If the vector is not normalized, that is the sum of the square of its three coordinates is not 1, it will be normalized internally. A non-normalizable vector, like the null vector, [0, 0, 0], will cause the rotation not to be applied, without invaliding the whole CSS property.

Syntax

rotate3d(x, y, z, a)

Values

x

Is a <number> describing the x-coordinate of the vector denoting the axis of rotation.

y

Is a <number> describing the y-coordinate of the vector denoting the axis of rotation.

z

Is a <number> describing the z-coordinate of the vector denoting the axis of rotation.

a

Is an <angle> representing the angle of the rotation. A positive angle denotes a clockwise rotation, a negative angle a counter-clockwise one.

Cartesian coordinates on R2	Homogenous coordinates on RP2	Cartesian coordinates on R3
This transform applies to the 3D space and cannot be represented on the plan.		$\left(\begin{array}{ccc}1+(1-cos(a))(x^2-1)& z·sin(a)+xy(1-cos(a))& -y·sin(a)+xz·(1-cos(a))\\ -z·sin(a)+xy·(1-cos(a))& 1+(1-cos(a))(y2-1)& x·sin(a)+yz·(1-cos(a))& ysin(a)\; +\; xz(1-cos(a))& -xsin(a)+yz(1-cos(a))& 1+(1-cos(a))(z2-1)& t\\ 0& 0& 0& 1\end{array}\right)$

Cartesian coordinates on R2	Homogenous coordinates on RP2	Homogenous coordinates on RP3
This transform applies to the 3D space and cannot be represented on the plan.

rotateX()

The rotateX()CSS function defines a transformation that moves the element around the abscissa without deforming it. The amount of movement is defined by the specified angle; if positive, the movement will be clockwise, if negative, it will be counter-clockwise.

The axis of rotation passes by the origin, defined by transform-origin CSS property.

rotateX(a)is a shorthand for rotate3D(1, 0, 0, a).

Syntax

rotateX(a)

Values

a

Is an <angle> representing the angle of the rotation. A positive angle denotes a clockwise rotation, a negative angle a counter-clockwise one.

Cartesian coordinates on R2	Homogenous coordinates on RP2	Cartesian coordinates on R3	Homogenous coordinates on RP3
This transform applies to the 3D space and cannot be represented on the plan.		$\left(\begin{array}{ccc}1& 0& 0\\ 0& cos(a)& sin(a)\\ 0& -sin(a)& cos(a)\end{array}\right)$	$\left(\begin{array}{cccc}1& 0& 0& 0\\ 0& cos(a)& sin(a)& 0\\ 0& -sin(a)& cos(a)& 0\\ 0& 0& 0& 1\end{array}\right)$

rotateY()

The rotateY()CSS function defines a transformation that moves the element around the ordinate without deforming it. The amount of movement is defined by the specified angle; if positive, the movement will be clockwise, if negative, it will be counter-clockwise.

The axis of rotation passes by the origin, defined by transform-origin CSS property.

rotateY(a)is a shorthand for rotate3D(0, 1, 0, a).

Syntax

rotateY(a)

Values

a

Is an <angle> representing the angle of the rotation. A positive angle denotes a clockwise rotation, a negative angle a counter-clockwise one.

Cartesian coordinates on R2	Homogenous coordinates on RP2	Cartesian coordinates on R3	Homogenous coordinates on RP3
This transform applies to the 3D space and cannot be represented on the plan.		$\left(\begin{array}{ccc}cos(a)& 0& sin(a)\\ 0& 1& 0\\ -sin(a)& 0& cos(a)\end{array}\right)$	$\left(\begin{array}{cccc}cos(a)& 0& sin(a)& 0\\ 0& 1& 0& 0\\ -sin(a)& 0& cos(a)& 0\\ 0& 0& 0& 1\end{array}\right)$

rotateZ()

The rotateZ()CSS function defines a transformation that moves the element around the z-axis without deforming it. The amount of movement is defined by the specified angle; if positive, the movement will be clockwise, if negative, it will be counter-clockwise.

The axis of rotation passes by the origin, defined by transform-origin CSS property.

rotateZ(a)is a shorthand for rotate3D(0, 0, 1, a).

Syntax

rotateZ(a)

Values

a

Is an <angle> representing the angle of the rotation. A positive angle denotes a clockwise rotation, a negative angle a counter-clockwise one.

Cartesian coordinates on R2	Homogenous coordinates on RP2	Cartesian coordinates on R3	Homogenous coordinates on RP3
This transform applies to the 3D space and cannot be represented on the plan.		$\left(\begin{array}{ccc}cos(a)& sin(a)& 0\\ -sin(a)& cos(a)& 0\\ 0& 0& 1\end{array}\right)$	$\left(\begin{array}{cccc}cos(a)& sin(a)& 0& 0\\ -sin(a)& cos(a)& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 1\end{array}\right)$

scale()

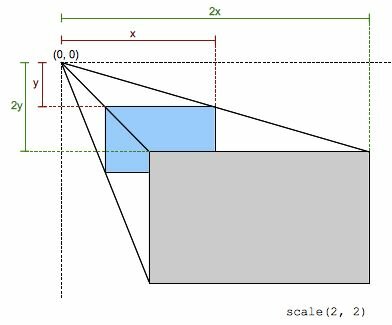
The scale() CSS function modify the size of the element. It can either augment or decrease its size and as the amount of scaling is defined by a vector, if can do so more in one direction than in another one.

This transformation is characterized by a vector whose coordinates define how much scaling is done in each direction. If both coordinates of the vector are equals, the scaling is uniform, or isotropic, and the shape of the element is preserved. In that case, the scaling function defines an homothetic transformation.

When outside the ]-1, 1[ range, the scaling enlarges the element in the direction of the coordinate; when inside the range, it shrinks the element in that direction. When equals to 1 it does nothing and when negative it performs a point reflection and the size modification.

Syntax

scale(sx) or
scale(sx, sy)

Values

sx

Is a <number> representing the abscissa of the scaling vector.

sy

Is a <number> representing the ordinate of the scaling vector. If not present, its default value is sx, leading to a uniform scaling preserving the shape of the element.

Cartesian coordinates on R2	Homogenous coordinates on RP2	Cartesian coordinates on R3	Homogenous coordinates on RP3
$\left(\begin{array}{cc}sx& 0\\ 0& sy\end{array}\right)$	$\left(\begin{array}{cc}sx0& 0\\ 0sy& 0\\ 0& 0& 1\end{array}\right)$	$\left(\begin{array}{cc}sx0& 0\\ 0sy& 0\\ 0& 0& 1\end{array}\right)$	$\left(\begin{array}{ccc}sx0& 0& 0\\ 0& sy& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right)$
	[sx 0 0 sy 0 0]

scale3d()

The scale3d() CSS function modifies the size of an element. Because the amount of scaling is defined by a vector, it can resize different dimensions at different scales.

This transformation is characterized by a vector whose coordinates define how much scaling is done in each direction. If all three coordinates of the vector are equals, the scaling is uniform, or isotropic, and the shape of the element is preserved. In that case, the scaling function defines an homothetic transformation.

When outside the [-1, 1] range, the scaling enlarges the element in the direction of the coordinate; when inside the range, it shrinks the element in that direction. When equals to 1 it does nothing and when negative it performs a point reflection and the size modification.

Syntax

scale3d(sx, sy, sz)

Values

sx

Is a <number> representing the abscissa of the scaling vector.

sy

Is a <number> representing the ordinate of the scaling vector.

sz

Is a <number> representing the z-component of the scaling vector.

Cartesian coordinates on R2	Homogenous coordinates on RP2	Cartesian coordinates on R3	Homogenous coordinates on RP3
This transform applies to the 3D space and cannot be represented on the plan.		$\left(\begin{array}{cc}sx0& 0\\ 0sy& 0\\ 0& 0& sz\end{array}\right)$	$\left(\begin{array}{ccc}sx0& 0& 0\\ 0sy& 0& 0\\ 0& 0& sz& 0\\ 0& 0& 0& 1\end{array}\right)$

scaleX()

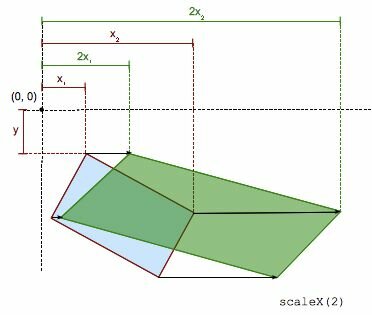The scaleX() CSS function modifies the abscissa of each element point by a constant factor, except if this scale factor is 1, in which case the function is the identity transform. The scaling is not isotropic and the angles of the element are not conserved.

scaleX(sx) is a shorthand for scale(sx, 1) or for scale3d(sx, 1, 1).

scaleX(-1) defines an axial symmetry with a vertical axis passing by the origin (as specified by the transform-origin property).

Syntax

scaleX(s)

Values

s

Is a <number> representing the scaling factor to apply on the abscissa of each point of the element.

Cartesian coordinates on R2	Homogenous coordinates on RP2	Cartesian coordinates on R3	Homogenous coordinates on RP3
$\left(\begin{array}{cc}s& 0\\ 0& 1\end{array}\right)$	$\left(\begin{array}{cc}s0& 0\\ 01& 0\\ 0& 0& 1\end{array}\right)$	$\left(\begin{array}{cc}s0& 0\\ 01& 0\\ 0& 0& 1\end{array}\right)$	$\left(\begin{array}{ccc}s0& 0& 0\\ 01& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right)$
	[s 0 0 1 0 0]

scaleY()

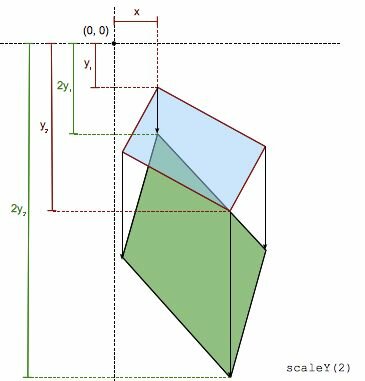
The scaleY() CSS function modifies the ordinate of each element point by a constant factor except if this scale factor is 1, in which case the function is the identity transform. The scaling is not isotropic and the angles of the element are not conserved.

scaleY(sy) is a shorthand for scale(1, sy) or for scale3d(1, sy, 1).

scaleY(-1) defines an axial symmetry with an horizontal axis passing by the origin (as specified by the transform-origin property).

Syntax

scaleY(s)

Values

s

Is a <number> representing the scaling factor to apply on the ordinate of each point of the element.

Cartesian coordinates on R2	Homogenous coordinates on RP2	Cartesian coordinates on R3	Homogenous coordinates on RP3
$\left(\begin{array}{c}10\\ 0& s\end{array}\right)$	$\left(\begin{array}{cc}10& 0\\ 0s& 0\\ 0& 0& 1\end{array}\right)$	$\left(\begin{array}{cc}10& 0\\ 0s& 0\\ 0& 0& 1\end{array}\right)$	$\left(\begin{array}{ccc}10& 0& 0\\ 0s& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right)$
	[1 0 0 s 0 0]

scaleZ()

The scaleZ() CSS function modifies the z-coordinate of each element point by a constant facto, except if this scale factor is 1, in which case the function is the identity transform. The scaling is not isotropic and the angles of the element are not conserved.

scaleZ(sz) is a shorthand for scale3d(1, 1, sz).

scaleZ(-1) defines an axial symmetry along the z-axis passing by the origin (as specified by the transform-origin property).

Syntax

scaleZ(s)

Values

s

Is a <number> representing the scaling factor to apply on the z-coordinate of each point of the element.

Cartesian coordinates on R2	Homogenous coordinates on RP2	Cartesian coordinates on R3	Homogenous coordinates on RP3
This transform applies to the 3D space and cannot be represented on the plan.		$\left(\begin{array}{cc}10& 0\\ 01& 0\\ 0& 0& s\end{array}\right)$	$\left(\begin{array}{ccc}10& 0& 0\\ 01& 0& 0\\ 0& 0& s& 0\\ 0& 0& 0& 1\end{array}\right)$

skew()

The skew() CSS function is a shear mapping, or transvection, distorting each point of an element by a certain angle in each direction. It is done by increasing each coordinate by a value proportionate to the specified angle and to the distance to the origin. The more far from the origin, the more away the point is, the greater will be the value added to it.

Syntax

skew(ax)       or
skew(ax, ay)

Values

ax

Is an <angle> representing the angle to use to distort the element along the abscissa.

ay

Is an <angle> representing the angle to use to distort the element along the ordinate.

Cartesian coordinates on R2	Homogenous coordinates on RP2	Cartesian coordinates on R3	Homogenous coordinates on RP3
$\left(\begin{array}{c}1tan(ax)\\ tan(ay)1\end{array}\right)$	$\left(\begin{array}{cc}1tan(ax)& 0\\ tan(ay)1& 0\\ 0& 0& 1\\ \end{array}\right)$	$\left(\begin{array}{cc}1tan(ax)& 0\\ tan(ay)1& 0\\ 0& 0& 1\end{array}\right)$	$\left(\begin{array}{ccc}1tan(ax)& 0& 0\\ tan(ay)1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right)$
	[1 tan(ay) tan(ax) 1 0 0]

skewX()

The skewX() CSS function is an horizontal shear mapping distorting each point of an element by a certain angle in the horizontal direction. It is done by increasing the abscissa coordinate by a value proportionate to the specified angle and to the distance to the origin. The more far from the origin, the more away the point is, the greater will be the value added to it.

Syntax

skewX(a)

Values

a

Is an <angle> representing the angle to use to distort the element along the abscissa.

Cartesian coordinates on R2	Homogenous coordinates on RP2	Cartesian coordinates on R3	Homogenous coordinates on RP3
$\left(\begin{array}{c}1tan(ay)\\ 01\end{array}\right)$	$\left(\begin{array}{cc}1tan(ay)& 0\\ 01& 0\\ 0& 0& 1\end{array}\right)$	$\left(\begin{array}{cc}1tan(ay)& 0\\ 01& 0\\ 0& 0& 1\end{array}\right)$	$\left(\begin{array}{ccc}1tan(ay)& 0& 0\\ 01& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right)$
	[1 0 tan(a) 1 0 0]

skewY()

The skewY() CSS function is an vertical shear mapping distorting each point of an element by a certain angle in the vertical direction. It is done by increasing the ordinate coordinate by a value proportionate to the specified angle and to the distance to the origin. The more far from the origin, the more away the point is, the greater will be the value added to it.

Syntax

skewY(a)

Values

a

Is an <angle> representing the angle to use to distort the element along the ordinate.

Cartesian coordinates on R2	Homogenous coordinates on RP2	Cartesian coordinates on R3	Homogenous coordinates on RP3
$\left(\begin{array}{c}10\\ tan(ax)1\end{array}\right)$	$\left(\begin{array}{cc}10& 0\\ tan(ax)1& 0\\ 0& 0& 1\end{array}\right)$	$\left(\begin{array}{cc}10& 0\\ tan(ax)1& 0\\ 0& 0& 1\end{array}\right)$	$\left(\begin{array}{ccc}10& 0& 0\\ tan(ax)1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right)$
	[1 tan(a) 0 1 0 0]

translate()

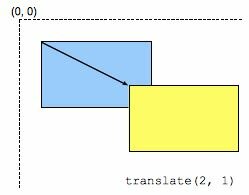The translate() CSS function moves the position of the element on the plane. This transformation is characterized by a vector whose coordinates define how much it moves in each direction.

Syntax

translate(tx)       or
translate(tx, ty)

Values

tx

Is a <length> representing the abscissa of the translating vector.

ty

Is a <length> representing the ordinate of the translating vector. If missing, it is assumed to be equals to tx :  translate(2) means translate(2, 2).

Cartesian coordinates on R2	Homogenous coordinates on RP2	Cartesian coordinates on R3	Homogenous coordinates on RP3
A translation is not a linear transform in R2 and cannot be represented using a matrix in the cartesian coordinates system.	$\left(\begin{array}{cc}10& tx\\ 01& ty\\ 0& 0& 1\end{array}\right)$	$\left(\begin{array}{cc}10& tx\\ 01& ty\\ 0& 0& 1\end{array}\right)$	$\left(\begin{array}{ccc}10& 0& tx\\ 01& 0& ty\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right)$
	[1 0 0 1 tx ty]

translate3d()

The translate3d() CSS function moves the position of the element in the 3D space. This transformation is characterized by a 3-dimension vector whose coordinates define how much it moves in each direction.

Syntax

translate3d(tx, ty, tz)

Values

tx

Is a <length> representing the abscissa of the translating vector.

ty

Is a <length> representing the ordinate of the translating vector.

tz

Is a <length> representing the z component of the translating vector. It can't be a <percentage> value; in that case the property containing the transform is considered invalid.

Cartesian coordinates on R2	Homogenous coordinates on RP2	Cartesian coordinates on R3	Homogenous coordinates on RP3
This transform applies to the 3D space and cannot be represented on the plan.		A translation is not a linear transform in R3 and cannot be represented using a matrix in the Cartesian coordinates system.	$\left(\begin{array}{ccc}10& 0& tx\\ 01& 0& ty\\ 0& 0& 1& tz\\ 0& 0& 0& 1\end{array}\right)$

translateX()

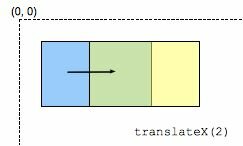The translateX() CSS function moves horizontally the element on the plane. This transformation is characterized by a <length> defining how much it moves horizontally.

translateX(tx) is a shortcut for translate(tx, 0).

Syntax

translateX(t)

Values

t

Is a <length> representing the abscissa of the translating vector.

Cartesian coordinates on R2	Homogenous coordinates on RP2	Cartesian coordinates on R3	Homogenous coordinates on RP3
A translation is not a linear transform in R2 and cannot be represented using a matrix in the cartesian coordinates system.	$\left(\begin{array}{cc}10& t\\ 01& 0\\ 0& 0& 1\end{array}\right)$	$\left(\begin{array}{cc}10& t\\ 01& 0\\ 0& 0& 1\end{array}\right)$	$\left(\begin{array}{ccc}10& 0& t\\ 01& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right)$
	[1 0 0 1 t 0]

translateY()

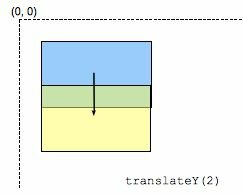The translateY() CSS function moves vertically the element on the plane. This transformation is characterized by a <length> defining how much it moves vertically.

translateY(ty) is a shortcut for translate(0, ty).

Syntax

translateY(t)

Values

t

Is a <length> representing the z-component of the translating vector. It can't be a <percentage> value; in that case the property containing the transform is considered invalid.

Cartesian coordinates on R2	Homogenous coordinates on RP2	Cartesian coordinates on R3	Homogenous coordinates on RP3
A translation is not a linear transform in R2 and cannot be represented using a matrix in the cartesian coordinates system.	$\left(\begin{array}{cc}10& 0\\ 01& t\\ 0& 0& 1\end{array}\right)$	$$ \left(\begin{array}{cc}10& 0\\ 01& t\\ 0& 0& 1\end{array}\right)$$	$\left(\begin{array}{ccc}10& 0& 0\\ 01& 0& t\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right)$
	[1 0 0 1 0 t]

translateZ()

The translateZ() CSS function moves the element along the z-axis of the 3D space. This transformation is characterized by a <length> defining how much it moves.

translateZ(tz) is a shorthand for translate3d(0, 0, tz).

Syntax

translateZ(t)

Values

t

Is a <length> representing the ordinate of the translating vector.

Cartesian coordinates on R2	Homogenous coordinates on RP2	Cartesian coordinates on R3	Homogenous coordinates on RP3
This transform applies to the 3D space and cannot be represented on the plan.		A translation is not a linear transform in R3 and cannot be represented using a matrix in the Cartesian coordinates system.	$\left(\begin{array}{ccc}10& 0& 0\\ 01& 0& 0\\ 0& 0& 1& t\\ 0& 0& 0& 1\end{array}\right)$